Correction - asymptote oblique
Exercice 1
On considère la fonction définie sur \(\mathbb{R}\backslash \{-1\}\) par : $$ f (x) = \frac{x^2-x-3}{x+1} $$
1
Il s'agit d'une forme indéterminée. On factorise le numérateur par \(x^2\) et le dénominateur par \(x\) : $$ \begin{array}{lll} f (x) & = & \frac{x^2 \left ( 1 - \frac{1}{x} - \frac{3}{x}\right )}{x \left ( 1 + \frac{1}{x}\right )} \\ & = & \frac{x \left ( 1 - \frac{1}{x} - \frac{3}{x}\right )}{\left ( 1 + \frac{1}{x}\right )} \\ \end{array} $$ On sait que : $$ \lim\limits_{x \rightarrow +\infty} x = +\infty $$ et que : $$ \lim\limits_{x \rightarrow +\infty} \frac{\left ( 1 - \frac{1}{x} - \frac{3}{x}\right )}{\left ( 1 + \frac{1}{x}\right )} = \frac{1}{1} = 1 $$ donc, on en déduit la limite du quotient : $$ \lim\limits_{x \rightarrow +\infty} f (x) = +\infty $$ On raisonne de même en \(- \infty\) et donc : $$ \lim\limits_{x \rightarrow -\infty} f (x) = -\infty $$
2
Limite à gauche (en \(-1^-\)) :
Limite du numérateur : $$ \lim\limits_{x \rightarrow -1^-} x^2-x-3 = (-1)^2 - (-1) - 3 = -1 $$ Limite du dénominateur : $$ \lim\limits_{x \rightarrow -1^-} x+1 = 0^- $$ donc, on en déduit la limite du quotient : $$ \lim\limits_{x \rightarrow -1^-} f (x) = +\infty $$ On raisonne de même en \(-1^+\). Comme \(\lim\limits_{x \rightarrow -1^+} x^2-x-3 = -1\) et \(\lim\limits_{x \rightarrow -1^+} x+1 = 0^+\) : $$ \lim\limits_{x \rightarrow -1^-} f (x) = -\infty $$3
La courbe \(C_f\) possède une asymptote verticale d'équation \(x=-1\) d'après la question 2.
4
On calcule la dérivée de \(f\) sur \(\mathbb{R}\backslash \{-1\}\) : \frac{x^2-x-3}{x+1} $$ \begin{array}{lll} f' (x) & = & \frac{(2x-1)(x+1) - (x^2-x-3)\times 1}{(x+1)^2} \\ & = & \frac{ 2x^2 + 2x - x - 1 - x^2 + x +3}{(x+1)^2} \\ & = & \frac{ x^2 + 2x + 4}{(x+1)^2} \\ \end{array} $$ On étudie le numérateur (polynôme du second degré), en calculant le discriminant : $$ \Delta = 2^2 - 4 \times 1 \times 4 = -12 $$
Il n'y a pas de racine réelle, le polynôme est positif pour tout \(x\) réel.
De plus, le numérateur est toujours positif et s'annule en -1. On en déduit le tableau de variation :
$$ \begin{array}{c|lcccr|} x & -\infty & & & -1 & & & +\infty \\ \hline x^2 + 2x + 4 & & + & & & & + & \\ \hline (x+1)^2 & & + & & 0 & & + & \\ \hline f'(x) & & + & & || & & + & \\ \hline & & & +\infty&|| & & & +\infty \\ f (x) & & \nearrow & &|| & & \nearrow & \\ & -\infty & & &|| &-\infty & & \\ \hline \end{array} $$5
Soit \((D)\) la droite d'équation \(y=x-2\)
a
On calcule : $$ \begin{array}{lll} f (x) - (x-2) & = & \frac{x^2-x-3}{x+1} - (x-2) \\ & = & \frac{x^2-x-3}{x+1} - \frac{(x-2)(x+1)}{x-2} \\ & = & \frac{x^2-x-3 - (x-2)(x+1)}{x+1}\\ & = & \frac{x^2-x-3 - (x^2+x-2x-2)}{x+1}\\ & = & \frac{x^2-x-3 - (x^2-x-2)}{x+1}\\ & = & \frac{x^2-x-3 - x^2+x+2}{x+1}\\ & = & \frac{-1}{x+1}\\ \end{array} $$
b
Pour étudier la position de \(C_f\) par rapport à \((D)\), on étudie le signe de \(f (x) - (x-2)\), c'est à dire le signe de \(\frac{-1}{(x+1)}\) d'après la question précédente : $$ \begin{array}{c|lcccr|} x & -\infty & & & -1 & & +\infty \\ \hline -1 & & - & & - & \\ \hline x+1 & & - & 0 & + & \\ \hline f (x) - (x-2) & & + & || & - & \\ \hline \end{array} $$
\(f (x) - (x-2) \gt 0\) sur \(]-\infty;-1[\), donc \(C_f\) est au dessus de \((D)\) sur \(]-\infty;-1[\)
\(f (x) - (x-2) \lt 0\) sur \(]-1;+\infty[\), donc \(C_f\) est en dessous de \((D)\) sur \(]-1;+\infty[\)
c
On calcule les limites de \(\frac{-1}{x+1}\) en \(-\infty\) et \(+\infty\) : $$ \lim\limits_{x \rightarrow -\infty} x+1 = -\infty $$ Donc : $$ \lim\limits_{x \rightarrow -\infty} x+1 = 0 $$ et de même : $$ \lim\limits_{x \rightarrow +\infty} x+1 = 0 $$ On en déduit que vers l'infini, la courbe \(C_f\) et la droite \((D)\) se rapprochent infiniment. On dit que \((D)\) est une asymptote oblique de la courbe \(C_f\).
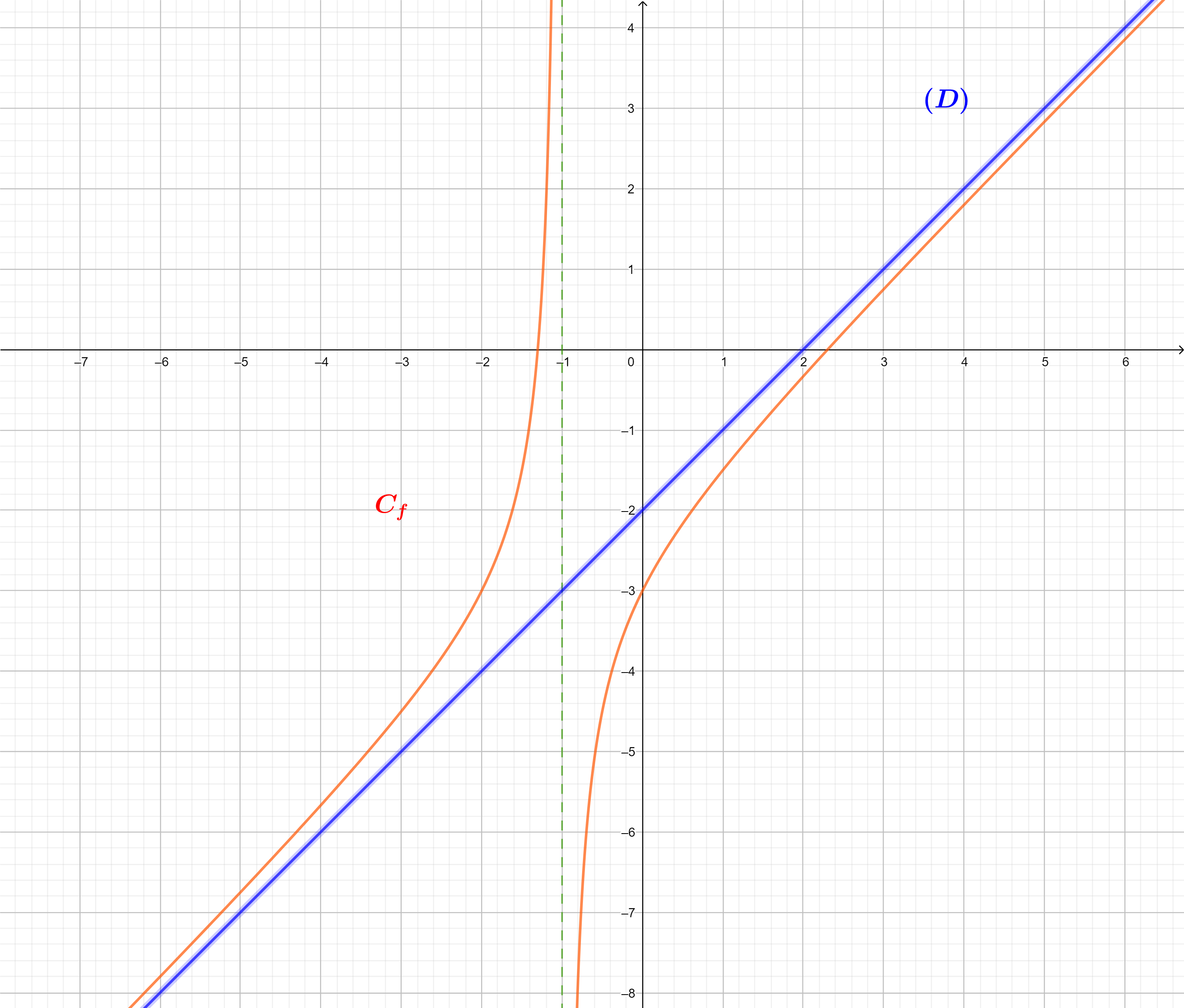
On peut vérifier graphiquement les résultats obtenus sur le graphique suivant où apparaissent \(C_f\), l'asymptote verticale et \((D)\) l'asymptote oblique :